函数式初识(6) - 组合

在Point-free的文章中我们简单的提到过组合(compose)技术，现在我们来做一些比较沉入的了解。

function minus2(x) { return x - 2; }
function triple(x) { return x * 3; }
function increment(x) { return x + 1; }
 
// 算总价
let temp = increment(4);
temp = triple(temp);
totalCost = basePrice + minus2(temp);

可以看到这段代码其实就是在利用一个中间变量去计算最终的购物总价，为了理解这段代码，你需要将所有东西串联起来，理解了第一个去理解第二个，然后将第一个和第二个联合起来，就得到了中间那个变量是个啥，然后要将之前的基础价格加起来也就是说你需要将所有东西放到一起来理解 — 中间变量，基础价格，所有的函数。

这个时候我想跟大家介绍一种思想 — 抽象(abstraction)。抽象指的是在两个原本“耦合”在一起的事物中加入一个语义边界使其分离。那么语义边界是啥？在下面的例子里我们来慢慢揭晓。其实抽象并不是要将与主体不相关的东西隐藏起来，它更希望是将它们独立分离开。使我们能够对两个或多个事物进行独立思考并且不用考虑另外的事物对它的影响，更容易去分析和理解。所以对于第6行到第8行代码，我们要想办法分离他们，并不是说我们要隐藏。

接下来我需要你在代码和虚拟故事中不断切换自己的身份：

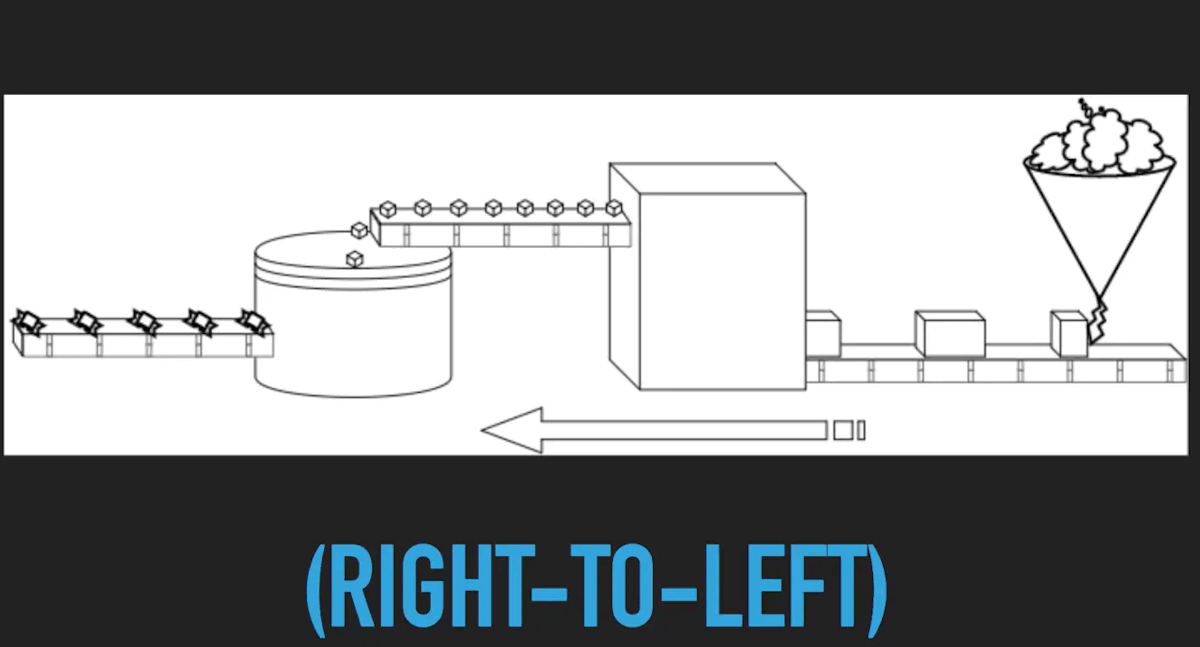
我们假设你是流水线上的一个工人，你的任务是维护和改造这条流水线。第一步我们将融化的巧克力倒进漏斗，然后千克力就被变成一个个大的巧克力方糖；然后进入下一个机器，这个机器将大的方糖切成小方糖；再然后小方糖进入最后一个机器，被做成糖果。

有一天，老板老找你说：小伙，我们这个机器供应不足啊，这不行啊，你想想办法，加加速，多做点，但是我没多余的厂房了，你自己想想办法哈。

我们回到代码里，想想那些中间变量。那些中间变量其实除了给我们增加理解负担以外并没有什么用了。所以，我们来看看能不能用一种大家常用的方式干掉它：

totalCost = basePrice + minus2(triple(increment(4)));

其实，这就是函数的组合 — 一个函数接收一个参数，然后将其唯一的返回值作为下一个函数的参数。那么这么来看，我们用这种方式干掉了中间变量，是不是就节省了很多空间呢？

然后我们回到工厂里，我们是不是就可以想象，如果我们能把工厂里的中间变量干掉，那是不是在节省了空间的同时我们还可以加快加工的速度呢？比如这样：

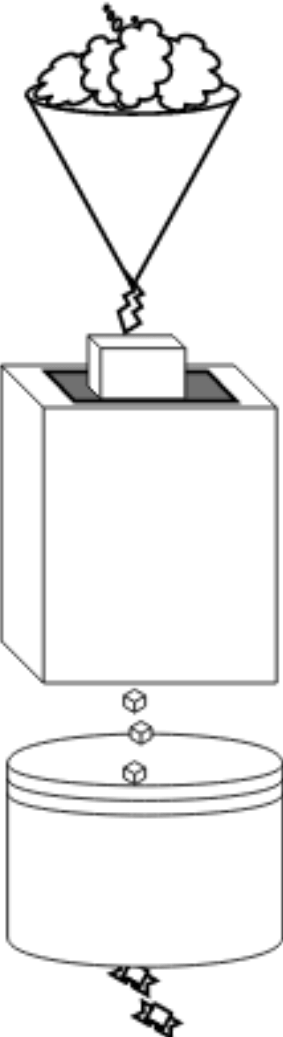
然后你的老板很开心，心里想996果然是有效果的。不过资本家嘛，肯定还有别的想法的，过了一段时间，老板又来找你了。老板说厂里的机器太多了，你是工头，你能清楚的记得啥时候按启动键，啥时候应该把料放到下一个机器里，但是流水线上的工人不知道哇，你能不能把流水线搞简单点，就一台机器，巧克力放进去，糖就出来了，这样可以减(ci)轻(tui)点工人的负担。这个时候该你犯嘀咕了，先不说能不能做到，就算能做到，中间某一步出问题了咋办？我把机器拆了去看哪出问题了？那我不得好好研究研究，不给自己挖坑，以后修机器咋整呢。

回到代码里，我们的代码也有相同的问题，这个时候我们的解决办法也很简单 — 函数提取：

function shippingRate(x) {
    return minus2(triple(increment(x)));
}
 
totalCost = basePrice + shippingRate(4);

所以在最后一行我们的代码就被拆分成两个部分了，比之前简洁了很多，这个时候其实我们已经做了一个完整的抽象。还记得上面说的语义边界吗？这里的语义边界就是函数名，语义边界将如何去做(函数定义)和做了什么(函数调用)做了分离。

回到工厂里来，是的没错，为了完成老板的任务，其实我们只需要在整个机器外边套一个大箱子就可以了，箱子上我们搞一个控制面板，方便我们修机器，对于工人来说，他们只需要打开开关，放入材料，所有的一切就可以自动运转了。就像这样：

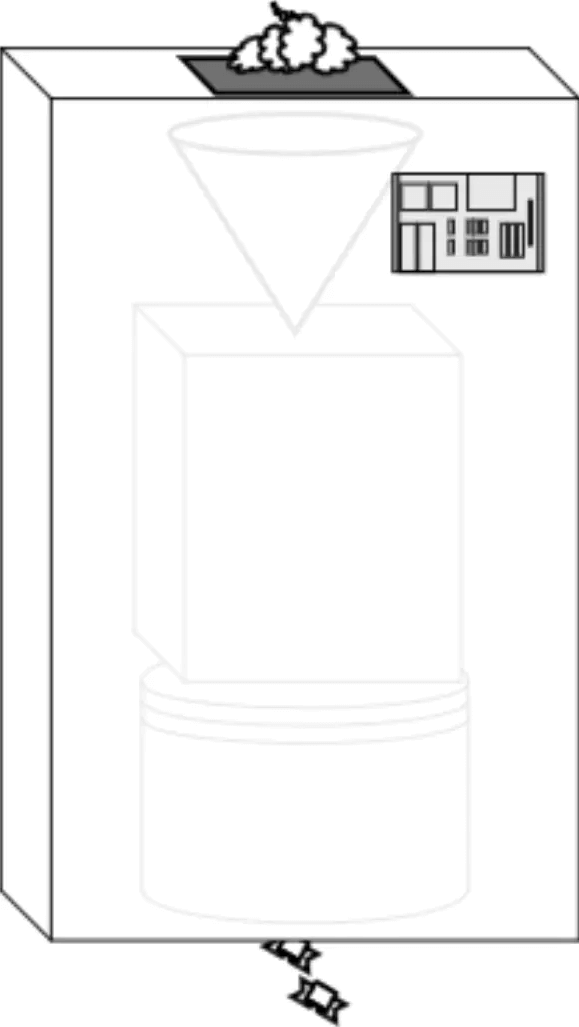
然后过了几天，老板想扩充市场了，他不但想做巧克力，还想做小黑兔奶糖，可能还要做别的玩意，可是他又不想买一堆新机器，成本太高了，他想让你改造发明下，能不能用机器去生产机器，我想做奶糖，就用大机器去生产一个奶糖机器，然后奶糖机器就可以用来做奶糖，想做巧克力就生产一个巧克力机器，然后就可以用它生产巧克力。

回到代码里来，在真实的代码环境中，如果真的需要我们计算消费价格，我们可能有许许多多的价格需要计算，那么为了计算这些价格，我们就需要定义许许多多的价格计算函数，那我们能不能定义一个“组合”函数去生成这一堆的函数呢？比如这样：

function composeThree(fn2, fn1, fn0) {
    return function composed(v) {
        return fn2(fn1(fn0(v)));
    }
}

然后我们的计算函数就可以这样定义：

const shippingRate = composeThree(minus2, triple, increment);
 
totalCost = basePrice + shippingRate(4);

于是利用我们已经定义好的“函数组件”，我们可以定义出各种各样的计算函数：

const internetShippingRate = composeThree(double, increment, minus1);
 
const xxxShippingRate = composeThree(increment, triple, minus4);

这样的定义不仅仅是Point-free风格的，而且要更加偏向于声明式，更易于理解。可以看出compose函数实际上是一个“从右到左”的执行过程，我们将最初的参数传给最右边的函数，计算后的返回值传入左边的函数，直到计算出最终结果。

其实组合就是一条声明式的数据流。数据经过了一系列的函数运算之后得到最终的返回值。所以其实组合的思想在于，你的所有程序都是一系列的数据流，你的任何程序都是拿到一个输入值，做一些事情，然后返回一个值，下一个部分再拿到这个值，以此反复。所以组合技术对于函数式编程是至关重要的。

最后一次，我们回到工厂里，按照代码里面的解决办法，其实我们的工厂就有了这么一个解决方案：

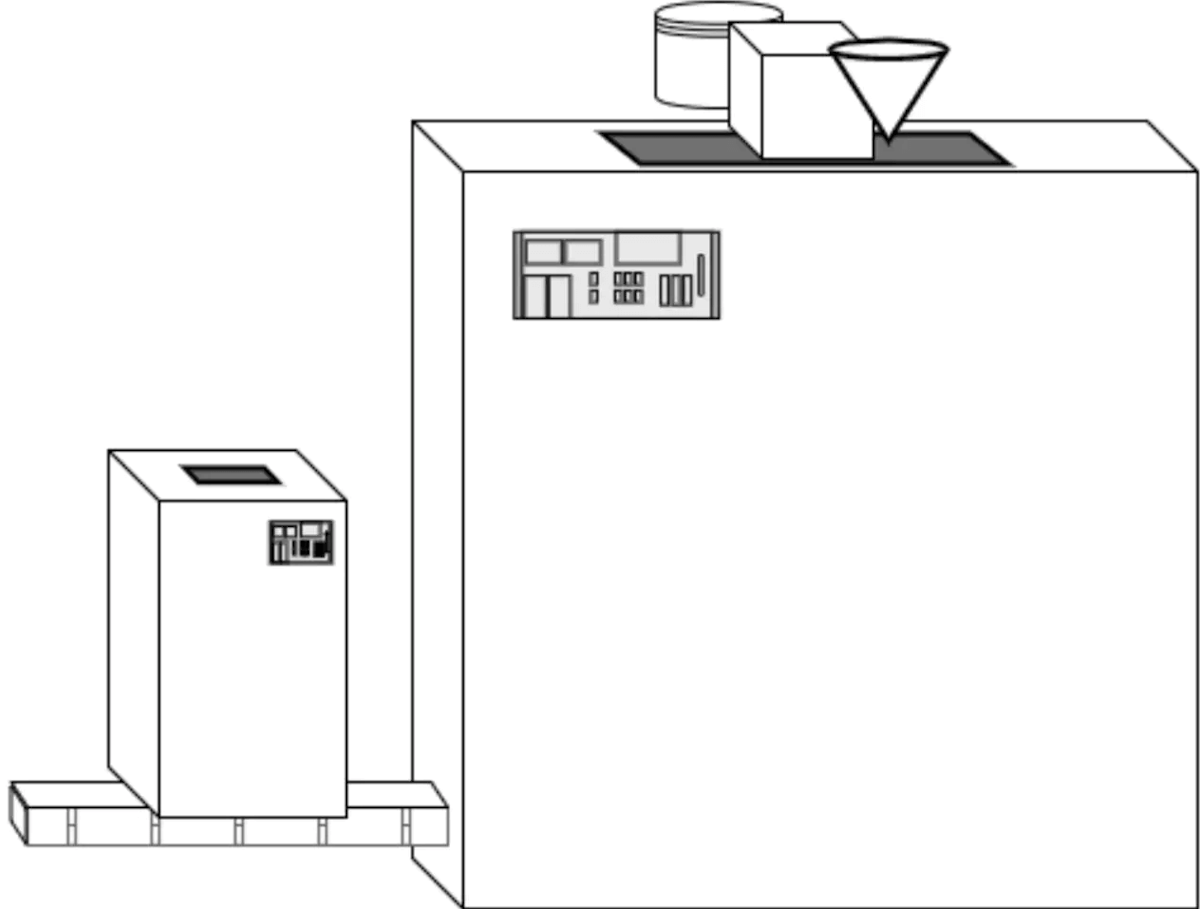
Pipe VS Compose

Compose是一种从右到左的定义方式，相对应的，Pipe是一种从左到右的定义方式。

function minus2(x) { return x - 2; }
function triple(x) { return x * 3; }
function increment(x) { return x + 1; }
 
const f = composeThree(minus2, triple, increment);
const p = pipeThree(increment, triple, minus2);
 
f(4); // 7
g(4); // 7

为什么有两个方向呢？我也不知道，只能说一个大概的理解。当我们有一组函数是这样调用的A(B(C()))，那么他们的执行顺序是 — C => B => A。表面上来看他们的执行顺序是从右到左的，但是其实是从内到外的。所以其实compose的参数顺序是符合真正的函数复合调用的书写顺序的。但是为了更加迎合我们的人脑思考，就有了Pipe，因为大脑一般会思考一个从左到右的执行顺序。

结合律与柯里化

众所周知，结合律也是数学中的一个定律。compose是严格遵守结合律的：

compose(fn1, compose(fn2, fn3)) === compose(compose(fn1, fn2), fn3);

所以组合就可以与柯里化完美运用：

function sum(x, y) { return x + y; }
function triple(x) { return x * 3; }
function divBy(y, x) { return x / y; }
 
divBy(2, triple(sum(3, 5))); // 12
 
sum = curry(2, sum);
divBy = curry(2, divBy);
 
compose(
    divBy(2),
    triple,
    sum(3)
)(5);
// 12

Point-free with composition

const mod2 = mod(2);
const eq1 = eq(1);
 
function isOdd(x) {
    return eq1(mod(x));
}
 
const isOdd = compose(eq1, mod2);
const isOdd = compose(eq(1), mod(2));